Pattern Matching Algorithms

Introduction

Pattern Searching algorithms are used to find a pattern or substring from another bigger string. There are different algorithms. The main goal is to design these types of algorithms to reduce the time complexity. The traditional approach may take lots of time to complete the pattern searching task for a longer text. The blog describes a few standard algorithms used for processing texts. They apply, for example, to the manipulation of texts (text editors), to the storage of textual data (text compression), and to data retrieval systems. The algorithms of the chapter are interesting in different respects.

First, they are basic components used in the implementations of practical software. Second, they introduce programming methods that serve as paradigms in other fields of computer science (system or software design). Third, they play an important role in theoretical computer science by providing challenging problems. 

In this blog, texts and elements of patterns are strings, which are finite sequences of symbols over a finite alphabet. Methods for searching patterns described by general regular expressions derive from standard parsing techniques. We focus our attention to the case where the pattern represents a finite set of strings. Although the latter case is a specialization of the former case, it can be solved with more efficient algorithms. Solutions to pattern matching in strings divide in two families.

 

Types Pattern Matching Algorithms

1. Fixed Patterns

1.1 Finite Automata algorithm for Pattern Searching 

In FA based algorithm, we preprocess the pattern and build a 2D array that represents a Finite Automata. Construction of the FA is the main tricky part of this algorithm. Once the FA is built, the searching is simple. In search, we simply need to start from the first state of the automata and the first character of the text. At every step, we consider next character of text, look for the next state in the built FA and move to a new state. If we reach the final state, then the pattern is found in the text.

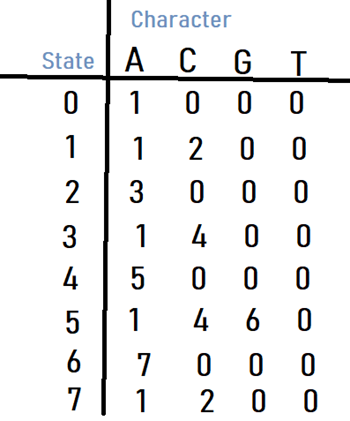
Fig 1.1 : FA for pattern ACACAGA

 

Fig 1.2 : Tabular representation of 

pattern ACACAGA

The above diagrams represent graphical and tabular representations of pattern ACACAGA.

Number of states in FA will be M+1 where M is length of the pattern. The main thing to construct FA is to get the next state from the current state for every possible character.

Explanation: Given a character x and a state k, we can get the next state by considering the string “pat [0..k-1]x” which is basically concatenation of pattern characters pat[0], pat[1] … pat[k-1] and the character x. The idea is to get length of the longest prefix of the given pattern such that the prefix is also suffix of “pat [0..k-1]x”. The value of length gives us the next state.

For Example: let us see how to get the next state from current state 5 and character ‘C’ in the above diagram. We need to consider the string, “pat [0..4]C” which is “ACACAC”. The length of the longest prefix of the pattern such that the prefix is suffix of “ACACAC”is 4 (“ACAC”). So, the next state (from state 5) is 4 for character ‘C’. 

Time Complexity Analysis:

For finite automata construction, the time complexity is O(M*K).

Where, 

M: Pattern length

K: is a number of different characters.

The complexity of main pattern searching is O(n).

 

Applications of FA:

• For the designing of lexical analysis of a compiler.
• For recognizing the pattern using regular expressions.
• Used in text editors.
• For the implementation of spell checkers.
• For the designing of the combination and sequential circuits using Mealy and Moore Machines.

1.2 Naive algorithm for Pattern Searching

Slide the pattern over text one by one and check for a match. If a match is found, then slides by 1 again to check for subsequent matches. 

The naïve approach tests all the possible placement of Pattern P [1.......m] relative to text T [1......n]. We try shift s = 0, 1.......n-m, successively and for each shift s.

Compare T [s+1.......s+m] to P [1......m].

The naïve algorithm finds all valid shifts using a loop that checks the condition P [1.......m] = T [s+1.......s+m] for each of the n - m +1 possible value of s

 

Naive - String - Matcher (T, P)

 1. n ← length [T]

 2. m ← length [P]

 3. for s ← 0 to n -m

 4. do if P [1.....m] = T [s + 1....s + m]

 5. then print "Pattern occurs with shift"

Fig 1.2: Naive algorithm

1.3 Rabin-Karp algorithm 

The Naive String Matching algorithm slides the pattern one by one. After each slide, it one by one checks characters at the current shift and if all characters match then prints the match.

Like the Naive Algorithm, Rabin-Karp algorithm also slides the pattern one by one. But unlike the Naive algorithm, the Rabin Karp algorithm matches the hash value of the pattern with the hash value of the current substring of text, and if the hash values match then only it starts matching individual characters.

The Rabin Karp algorithm needs to calculate hash values for the following strings.

1. Pattern itself
2. All the substrings of the text of length m.

Hashing provides a simple method for avoiding a quadratic number of symbol comparisons in most practical situations. Instead of checking at each position p of the window on the text whether the pattern occurs here or not, it seems to be more efficient to check only if the factor of the text delimited by the window, namely, y[p .. p + m − 1], “looks like” x. In order to check the resemblance between the two strings, a hash function is used. But, to be helpful for the string-matching problem, the hash function should be highly discriminating for strings. 

A good hash function reduces the number of spurious hits. Spurious hits occurs when the hash value of the pattern string matches with hash value of substring of text even though the substring is not equal to pattern string. Spurious hits greatly increases the time complexity of the algorithm so in order to have a better performing algorithm we minimize the number of spurious hits by using modulus.

 

Fig 1.3 : Rabin-Karp algorithm

Analysis of Rabin-Karp Algorithm

1. Time Complexity: The best case and worst case time complexity of Robin-Karp algorithm is O(m+n-1) and O(mn), where 'm' and 'n' are the length of pattern and substring of text respectively. 
2. Space Complexity: We have a constant space complexity of O(1), meaning here we don’t use any extra space to get the final result. Only the hash values and some more extra variables are being stored in each iteration of the algorithm.

Applications of Rabin-Karp Algorithm

• It is used in plagiarism detecting algorithms since it is able to rapidly search through large volumes of text without really caring about the punctuation of the sentences.
• It is generally the preferred algorithm for multiple pattern search. 

1.4 The Knuth-Morris-Pratt (KMP)Algorithm

Knuth-Morris and Pratt introduce a linear time algorithm for the string matching problem. A matching time of O (n) is achieved by avoiding comparison with an element of 'S' that has previously been involved in comparison with some element of the pattern 'p' to be matched. i.e., backtracking on the string 'S' never occurs

Components of KMP Algorithm

1. The Prefix Function (Π): The Prefix Function, Π for a pattern encapsulates knowledge about how the pattern matches against the shift of itself. This information can be used to avoid a useless shift of the pattern 'p.' In other words, this enables avoiding backtracking of the string 'S.'
2. The KMP Matcher: With string 'S,' pattern 'p' and prefix function 'Π' as inputs, find the occurrence of 'p' in 'S' and returns the number of shifts of 'p' after which occurrences are found.

The KMP matching algorithm uses the degenerating property (pattern having same sub-patterns appearing more than once in the pattern) of the pattern and improves the worst case complexity to O(n). The basic idea behind KMP’s algorithm is: whenever we detect a mismatch (after some matches), we already know some of the characters in the text of the next window. We take advantage of this information to avoid matching the characters that we know will anyway match.

Fig 1.4: KMP Algorithm

2. Suffix Automaton

A suffix automaton for a given string ss is a minimal DFA (deterministic finite automaton / deterministic finite state machine) that accepts all the suffixes of the string ss. A suffix automaton is an oriented acyclic graph. The vertices are called states, and the edges are called transitions between states. One of the states t0t0 is the initial state, and it must be the source of the graph (all other states are reachable from t0t0).  

A suffix automaton is a powerful data structure that allows solving many string-related problems. Intuitively a suffix automaton can be understood as a compressed form of all substrings of a given string. An impressive fact is that the suffix automaton contains all this information in a highly compressed form. 

In other words:

• A suffix automaton is an oriented acyclic graph. The vertices are called states, and the edges are called transitions between states.
• One of the states t0 is the initial state, and it must be the source of the graph (all other states are reachable from t0).
• Each transition is labeled with some character. All transitions originating from a state must have different labels.
• One or multiple states are marked as terminal states. If we start from the initial state t0 and move along transitions to a terminal state, then the labels of the passed transitions must spell one of the suffixes of the string s. Each of the suffixes of s must be spellable using a path from t0 to a terminal state.
• The suffix automaton contains the minimum number of vertices among all automata satisfying the conditions described above.

For example, you can search for all occurrences of one string in another, or count the amount of different substrings of a given string. Both tasks can be solved in linear time with the help of a suffix automaton. 

 

Fig 2.1 : Suffix Automaton

Algorithm of Suffix Automaton:

• Let last be the state corresponding to the entire string before adding the character c. (Initially we set last=0, and we will change last in the last step of the algorithm accordingly.)
• Create a new state cur, and assign it with len(cur)=len(last)+1. The value link(cur) is not known at the time.
• Now we to the following procedure: We start at the state last. While there isn't a transition through the letter c, we will add a transition to the state cur, and follow the suffix link. If at some point there already exists a transition through the letter c, then we will stop and denote this state with p.
• If it haven't found such a state p, then we reached the fictitious state −1, then we can just assign link(cur)=0 and leave.
• Suppose now that we have found a state p, from which there exists a transition through the letter c. We will denote the state, to which the transition leads, with q.
• Now we have two cases. Either len(p)+1=len(q), or not.
• If len(p)+1=len(q), then we can simply assign link(cur)=q and leave.
• Otherwise it is a bit more complicated. It is necessary to clone the state q: we create a new state clone, copy all the data from q (suffix link and transition) except the value len. We will assign len(clone)=len(p)+1. After cloning we direct the suffix link from cur to clone, and also from q to clone. Finally we need to walk from the state p back using suffix links as long as there is a transition through c to the state q, and redirect all those to the state clone.
• In any of the three cases, after completing the procedure, we update the value last with the state cur.

Applications of Suffix Automaton:

• It is used for checking for occurrence of text.
• It remembers the number of different substring encountered.
• It is used to identify the longest common substring of two strings.

Conclusion

Nowadays, the majority of work is done on the internet, with users mostly using search engines. The most effective method for searching is pattern matching. Each algorithm has unique properties. The search algorithms we covered in this blog post are superior to others in this aspect of searching. We concentrated on the complexity of each approach, finding that the Rabin-Karp algorithm had a lower pre-processing time complexity while the Knuth-Morris-Pratt algorithm had a lower time complexity. If an effective algorithm is applied, exact string pattern matching's time performance can be significantly enhanced.

Thank you for reading till the end! :)

Authors:

Deven Bhadane, Aniruddha Bargaje, Tejas Bhandari, Shubham Bodake and Ranjana Burange